Atomic Number (Z) or Proton Number
Definition
Atoms of each element contain a characteristic number of protons. In fact, the number of protons determines what atom we are looking at (e.g., all atoms with six protons are carbon atoms); the number of protons in an atom is called the atomic number. In contrast, the number of neutrons for a given element can vary to produce isotopes. The number of electrons can also be different in atoms of the same element, thus producing ions (charged atoms). For instance, iron, Fe, can exist in its neutral state, or in the +2 and +3 ionic states.
“The number of protons present in the nucleus of an atom is called Atomic Number (denoted as Z)”. For this reason, it's sometimes called the proton number.
OR
“The number of electrons revolving in the orbits of neutral atom is called Atomic Number (as neutral atoms of an element contain an equal number of protons and electrons).
Atomic Number (Z) = Number of Protons (P) = Number of electrons (e)
All the atoms of a particular element have the same number of protons, and hence the same atomic number but atoms of different elements have different atomic numbers.
For example, all carbon atoms have the atomic number of 6, whereas all atoms of Oxygen have 8 protons in their nucleus.
Representation
Atomic number is written as SUBSCRIPT on the LEFT HAND SIDE of the chemical symbol of element. e.g. 3Li, 6C, 7N etc.
Origin of Symbol Z
“Atomic number" in German is "Atomzahl", so the Z symbol for atomic number probably comes from "Zahl" (meaning number).
The letter Z is one of the signs for the highest god in Greek mythology, Zeus.
In modern physics Z represents the greatest energy, nuclear power, in its potential form, nuclear charge."
Example
1. Atomic number of hydrogen is 1 because its nucleus contains 1 proton.
2.Atomic number of chlorine is 17 owing to the presence of 17 protons.
Range of Atomic Number
Because protons are units of matter, atomic numbers are always whole numbers. At present, they range from 1 (for hydrogen) to 118 (oganesson; the number of the heaviest known element).
Atomic number and mass number are always whole numbers because they are obtained by counting whole objects (protons, neutrons, and electrons).
Importance
1. It identifies the element i.e. it distinguishes one element from another. The proton number is unique to each element so no two elements have the same number of protons. Electrons come and go during chemical processes but the proton number doesn’t change.
2. The modern periodic table is organized according to increasing atomic number. Thus it determines the position of the element on the Periodic Table.
3. It is a key factor in determining the properties of an element. (Note, however, the number of valence electrons determines chemical bonding behavior).
Atomic Mass Number (A) or Nucleon Number
Definition
The sum of protons and neutrons in the nucleus of an atom is called Mass Number or Nucleon Number denoted as “A”.
OR
The total number of "nucleons" (Protons and Neutrons) in the nucleus of an atom is called mass number. (Protons and neutrons are collectively called nucleons).
Mass Number (A) = Number of protons (P) + Number of neutrons(n)
OR
Mass Number (A) = Atomic Number (Z) + Number of neutrons (n)
And
No of neutrons= Mass number (A) – Atomic number (Z)
e.g.
Mass number of Na is 23 because its nucleus contains 11 protons and 12 neutrons.
The nucleon number minus the proton number gives you the number of neutrons of an atom.
Representation
Mass number is written as superscript on the left hand side of the chemical symbol of element. e.g. 12C, 14N
Notation of Atom
To write the notation of an atom, we need to know the symbol of the element, the atomic number and the mass number. The mass number of the atom goes above the symbol (superscript) and the atomic number is written as a subscript below they symbol.
Calculating PEN (Protons-Electrons-Neutrons) Numbers
1. The atomic number is equal to the number of protons in an atom.
2. Since atoms are neutral, then it is also the same as the number of electrons.
3. The mass number is the number of protons plus neutrons.
4. The number of neutrons can thus be calculated by subtracting the atomic number from the mass number.
Example
Beryllium for example has an atomic mass of 4, therefore it has 4 protons and 4 electrons.
The mass number of beryllium is 9, so it has 9 – 4 = 5 neutrons.
The PEN numbers for beryllium are thus:
p = 4
e = 4
n = 9 – 4 = 5
Isotopes of Elements
Definition
The existence of isotopes of elements was first discovered by J.J. Thomson in 1913. The name of isotope was introduced by Soddy because they have the same atomic number and hence occupied the same place in the periodic table. (Isotope is a Greek word; iso = same; topos = place). Nearly all elements found in nature are mixture of several isotopes.
“Isotopes are atoms of the same element having SAME ATOMIC NUMBER but DIFFERENT MASS NUMBERS (atomic masses)”.
OR
“Isotopes are different forms of atoms of an element which have SAME NUMBER OF PROTONS (and also electrons) but DIFFERENT NUMBER OF NEUTRONS in their respective nuclei”.
For example carbon has three of isotopes namely carbon-12, carbon-13 and carbon-14.
Different isotopes of an element have same chemical properties due to their identical electronic configuration (i.e. same number of electrons in the shells) but they have different physical properties because of their different atomic masses.
Since the proton count establishes elemental identity, chemical traits of different isotopes of the same element tend to be the same. However, isotopes differ in respects of physical properties which depend on atomic mass.
The different number of neutrons, however, affects the stability and mass of the nucleus, sometimes creating a radioactive isotope, sometimes creating a non-radioactive (or stable) isotope.
Uses of Isotopes
1. As tracers in physical, chemical, biological, medical and metallurgical researches.
2. As therapeutic agent for diagnoses and treatments of various diseases like cancer as radioactive isotopes are easily detected and traced.
3. Electrical power generation.
Symbolic Representation of Isotopes
The symbol for an isotope is the chemical symbol (or word showing name of element) followed by a dash and then the mass number. So C-14 is the isotope of carbon which contains 6 protons, 6 electrons and 14 – 6 = 8 neutrons. It can also be written as 14C.
In denoting particular isotopes of an element, the following notation has been internationally adopted. The symbol of the element is written with atomic at the head and atomic number at the bottom. Alternatively, the name of the element is followed by the atomic with a hyphen (-) in between. Thus the isotopes of carbon with atomic number 6 having atomic masses of 12 and 14 may be written as:
12C or carbon-12 or C-12 reads ‘carbon twelve’ meaning isotope of carbon with a mass of approximately 12 amu.
Kinds of Isotopes
1. Natural non-radioactive
2. Natural Radioactive
3. Artificial Radioactive (made by neutron bombardment)
Classification of Elements on the Basis of Number of Isotopes
Important Points
1. Nearly all elements found in nature are mixture of several isotopes.
2. There are 287 different isotopic species in nature.
3. Out of 92 elements, 23 elements have no isotopes, each consisting of only one kind of atoms e.g. 4Be,9F, 11Na, 13Al, 15P, 21Sc, 25Mn, 27Co, 33As, 39Y, 41Nb (niobium), 45Rh (rhodium), 53I, 55Cs, 59Pr (praseodymium), 65Tb (terbium), 69Tm (thulium), 67Ho (Holmium), 79Gold (Au), 83Bi, 87Fr, Actinum(89Ac), 90Th, Protactinium (91Pa). The remaining elements have 2 to 10 isotopes each.
NOTE
It is strictly improper to refer to elements that exist in only one atomic form as having “one isotope”; actually such elements like Be, F, Na, Al, P, Sc, Mn, Co, As, Y, Nb, Rh, I, Cs, Pr, Tb, Ho, Tm, Bi, Ac, Th, Pa have no isotopes i.e. they have no other atomic form that is like them in all respects except mass. The term isotopes require the existence of at least two atomic forms of an element; in the same sense that the word twin requires the existence of a pair. Recently the term mono-isotopic is evolved for elements found in nature as a single atomic (isotopic) form.
4. The heavier isotopes of elements usually occur very rarely in the atomic population (e.g. 1 part in 4500 for 2H, 1 part in 140 for U-235; in the exceptional case of chlorine, the ratio of isotopes 35 and 37 is about 3:1).
5. The isotopes with even atomic number and even atomic masses are more abundant in nature.
6.Different isotopes of an element occur in different amount or isotopic abundances.
7. To work out the relative atomic mass of an element, we need to find the average mass of all its isotopes which involves two steps:
(i) Multiply each relative isotopic mass by its isotopic abundance and add up the results.
(ii) Divide the result by the sum of the abundances. (If the abundances are given as percentages, this will be 100).
Contrary to Dalton’s atomic theory, all atoms of a given element are not necessarily identical. In fact, most elements have been shown to be composed of two or more types of atoms mixed in a fixed proportion.
(i) The different atoms of such an element contain equal number of protons and, therefore, have the same atomic number.
(ii) The atoms which vary from one have different number of neutrons in the nucleus. Thus they have different atomic masses.
Isotopes of Hydrogen
There are three isotopes of hydrogen namely protium or ordinary hydrogen, deuterium or heavy hydrogen, tritium or radioactive hydrogen. Protium is by far the most abundant in natural hydrogen, deuterium about 0.0156 % and tritium only one out of 10, 000, 000 hydrogen atoms.
The atomic number of three isotopes of hydrogen is 1 while their mass numbers are 1, 2 and 3 respectively. Each of the three isotopes of hydrogen has one proton in the nucleus and one extra-nuclear electron. The nucleus of protium contains one proton only while the number of neutrons in deuterium and tritium is 1 and 2 respectively.
Isotopes of Carbon
There are two stable isotopes and one radioactive isotope of carbon. The carbon-12 contain 6 proton and 6 neutron, Carbon-13 possess 6 proton and 7 neutron, carbon-14 contain 6 proton and 8 neutron. Carbon 12 is the most abundant (98.889%) isotope.
Isotopes of Oxygen
Oxygen has three isotopes;
with the relative abundances of 99.759, 0.037 and 0.204 respectively.
The atomic number of each of these three isotopes of oxygen is 8 while their mass numbers are 16,17 and 18 respectively. Thus each of these isotopes has 8 extra nuclear electrons and 8 protons in the nucleus. The number of neutrons in O-16, O -17 and O -18 is 8, 9 and 10 respectively.
Isotopes of Neon
Neon has three isotopes;
with their percentage abundance 99.92, 0.257 and 8.82% respectively.
The atomic number of each of these three isotopes of neon is 10 while their mass numbers are 20, 21 and 22 respectively. Thus each of these isotopes has 10 extra nuclear electrons and ten protons in the nucleus. The number of neutrons in Ne-20, Ne-21 and Ne-22 is 10, 11 and 12 respectively.
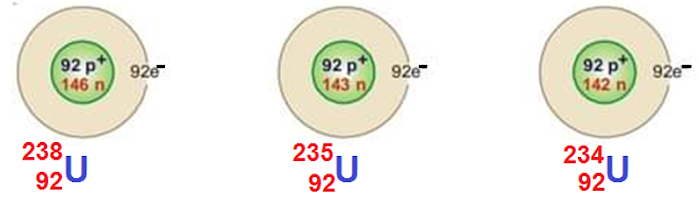
Isotopes of Uranium
There are three common isotopes of uranium with atomic number 92 and mass number 234, 235 and 238 respectively. The uranium is found 99% in nature.

Elements with no Isotopes or Mono-isotopic Elements
Nearly all elements found in nature are mixture of several isotopes. Out of 92 natural elements, only 23 elements have no isotopes, each consisting of only one kind of atom. The remaining 69 natural elements have from 2 to 10 isotopes.
Atomic Mass Unit (a.m.u or amu)
Unified atomic mass (u)
Atoms
are so tiny that the smallest speck of dust visible to the naked eye
contains about 106 atoms! Thus, the absolute masses of a
single atom (or nuclides and of elementary particles) in gram or kilogram is
much too small a number for convenience (it does not make sense to use the
same units like gram to measure the atomic mass that we use every day otherwise
their weight would be in billionths of a gram). Therefore, a unit of mass that
is better-sized for
measuring on the submicroscopic scale is needed. Chemists use a small unit
of mass called atomic mass unit (amu or u), also known as dalton (Da)
to express weight and masses of elementary particles.
An atomic mass unit (abbreviated as a.m.u.) is a physiochemical constant and it is
defined as one twelfth (1/12) of the mass of a single atom (the most abundant
lightest isotope) of carbon-12 (12C). It is the mass of 1/12 part of
carbon-12 atom. It is equal to one over Avogadro’s number when expressed in
gram.
[Because
the mass of an atom’s electrons is negligible compared with the mass of its
proton and neutrons, defining 1 amu as 1/12 the mass of a 12C atom
means that both protons and neutrons have a mass of almost exactly 1 amu].
1 amu is equivalent to 1.66 x 10–24 g OR 1.66 x 10–27
kg (which is approximately equal to the mass of one hydrogen atom).
Prior
to 1960, the amu was defined in terms of the mass of a 16O-isotope (1.6599
x 10–27 kg).
Derivation
of Atomic mass unit

Summary

Relation between amu and mass
in gram
1 amu = 1/12 mass of C12 atom ………………… (1)
1 mole of carbon-12 atom = 12 g ………………… (2)
1 mole = 6.023 x 1023 C-12 atoms ………………… (3)
Comparing
(1) and (2)
6.023 x 1023 C-12 atoms = 12 g
Divide
both sides by Avogadro’s number

Reason for taking caron-2
= 12 amu
1. Relative atomic mass of electron =
0.00055 amu approximately equal to 0 amu.
2. Relative atomic mass of proton =
1.0073 amu approximately equal to 1 amu
3. Relative atomic mass of neutron = 1.0087 amu approximately equal to 1 amu
4. Since C-12 atom has 6 protons and 6
neutrons, so mass of C-12 atom = 6 amu + 6 amu = 12 amu.
Atomic Mass or Relative atomic mass
Atoms
are so extremely tiny particles that we cannot weigh a single atom directly.
More ever, the mass of a single atom in gram is much too small a number for
convenience e.g. the mass of lightest known single hydrogen atom is 1.66 x
10–24 g and the mass of the heaviest known atom of uranium is 3.95
x 10–22 g (4 x 10–22 g). It
would be cumbersome to continually have to express such small masses in gram.
Clearly we cannot weigh any other kind of atom by orthodox weighing techniques.
However, it is possible to determine the mass of one atom relative to another
standard atom experimentally. Thus scientist needs special method to obtain
the mass of an atom by comparison to a standard mass. For this purpose in
1961, by an international agreement, the most stable lightest isotope of the
carbon called carbon-12 that has 6 protons and 6 neutrons having a mass of 12
atomic mass units or 12 amu (1.99 x 10–23 g) serves as the standard.
The mass of an atom depends upon the number of protons and neutrons present in
it.
The relative mass of the isotopes of an element as compared to
the mass of one atom of carbon-12 is known as Relative Atomic Mass i.e. it is number of times one atom of an element is heavier than
1/12th of one atom of standard carbon-12. The sum of number of
protons and neutrons gives the approximate atomic mass. This is called
Atomic Mass Number.
For example; the summation of proton and neutron of one atom of oxygen is 8 + 8 = 16. So its approximate atomic mass is 16 a.m.u. Similarly the atomic mass of sulphur is 32 a.m.u.
A hydrogen atom is only 8.400% as massive as the standard C-12, so atomic mass of hydrogen will be 0.08400 x 12.00 amu or 1.008 amu.
The most direct and
accurate device for determining atomic and molecular masses is mass
spectrometer.
Being
so small, atoms are also very light. Their masses range from 1 x 10-24
g to 1 x 10-22 g. It is impossible to weigh them out
individually, but we can accurately measure their relative masses i.e. how
heavy one atom as compared with another. The most accurate way of doing this is
by using a mass spectrometer. Originally, the atomic masses of all the elements
were compared with the mass of an atom of hydrogen.
This
is because hydrogen is the lightest element, so the relative atomic masses of
all other elements are greater than 1, which is convenient.
Because
of the existence of isotopes and the central importance of carbon in the masses
of organic compounds, the modern definition uses the isotope carbon-12 (12C)
as the standard of reference.
The
difference between the two definitions is small; since a carbon-12 atom has
almost exactly 12 times the average mass of a hydrogen atom (the actual ratio
is 11.91:1). Relative atomic mass is given the symbol Ar. Since it is the ratio
of two masses, it is a dimensionless quaintly – it has no units.
Although
we cannot use a laboratory balance to weigh out individual atoms, we can use it
to weigh out known ratios of atoms of various elements, as long as we know
their relative atomic masses. For example, if we know that the relative atomic
masses of carbon and magnesium are 12.0 and 24.0 respectively, we can be sure
that 12.0 g of carbon will contain the same number of atoms as 24.0 g of
magnesium. Similarly, 24.0 g (12.0 x 2) of carbon will contain twice the number
of atoms as 24.0 g of magnesium. Indeed, we can be certain that any mass of
carbon will contain twice the number of atoms as the same mass of magnesium,
since the mass of each carbon atom is only half the mass of a magnesium atom.
Similarly, if we know
that the relative atomic mass of helium is 4.0 (which is one-third the relative
atomic mass of carbon), we can deduce that identical masses of helium and
carbon will always contain three times as many helium atoms as carbon atoms.
Reason
for taking Carbon-12 as a Standard
1. High natural abundance; C-12 atom has
high natural abundance (98.89%)
2. High stability; C-12 is highly stable
due to which it has been considered as standard.
3. Least reactivity; Due to its least
reactive nature it is taken as standard.
4. Easily available
5. Not very reactive
6. Not inert
7. Easily separable from isotopes
8. 1/12 of weight of C-12 is comparable to
weight of H- atom (lightest atom)
Average Atomic Mass
We
know that atomic mass of carbon is 12.011 amu and is not exactly 12.00 amu. The
reason for the difference is that most naturally occurring elements (including
carbon) are mixtures of several isotopes with their varying percent
abundances. For example, naturally occurring carbon is composed of 98.889%
C-12 and 1.111% C-13.
An element’s atomic mass is a weighted average of the isotopic
masses of the element’s naturally occurring isotopes as compared to the mass of
one atom of C-12. The average atomic mass of an
element is determined by using the masses of its various isotopes and their
relative abundances.
Examples
1. Naturally occurring carbon is composed
of two isotopes, 12C with 98.892 % (98.889%) abundance (0.98892
fraction) and 13C with exact mass 13.0034 amu with 1.108 % (1.111%)
abundance (0.01108 fraction). Thus the average isotopic mass i.e. the atomic
weight of a large collection of carbon atoms is 12.011 amu.
2. Naturally occurring chlorine is a
mixture of two isotopes; 35Cl which has an abundance of 75.53% or
roughly 75% (0.7553 fraction) and an isotopic mass of 34.969 (35) amu and 37Cl
which has an abundance of 24.47% or roughly 25% (0.2447 fraction) and an
isotopic mass of 36.966 (37) amu. Thus the average isotopic mass i.e. the
atomic weight of a large collection of chlorine atoms is 35.46 amu.
3. Ordinary hydrogen consists of two
isotopes having atomic masses equal to 1.007825 amu and 2.01473 amu with
relative abundances of 99.98% and 0.0156% (i.e. in the ratio of 6400 : 1). Thus
atomic weight of hydrogen is:
Molecular Mass or Relative Molecular Mass (Mm)
The
term molecular mass can only be applied to covalent molecular compound
or some molecular elements. The term molecular mass cannot be used
strictly with ionic compounds as they do not comprise of discrete molecules.
Molecular Mass is number of times one molecule of a substance is heavier
than 1/12th of one atom of standard C-12 i.e. it is the average mass of a molecule of a substance (element or compound)
as compared with 1/12th mass of one atom of C-12. molecular Formula mass or Molecular
Mass (Mm) of a substance is the sum of atomic masses of all atoms
present in a molecule of a substance shown by its molecular formula.
The
relative molecular mass (Mm) of a substance is the relative atomic
masses (Ar) of all the atoms in its formula added together.
The Mm of a covalent compound is equal to the mass in
grams of 1 mole of that compound.
Examples
1. the
sum of atomic masses of H and O in H2O is = 2 x 1+ 1 x 16 = 18. So
its molecular mass is 18 a.m.u.
2. the
molecular formula mass of ozone (O3) is 16 x 3 = 48 a.m.u.
Formula Mass or
Relative Formula Mass
In
some crystalline compounds (NaCl, KCl, CaF2 etc.) there are no
discrete molecules but the atoms are bounded to one another in a network
structure as aggregate of positive and negative ions. Such compounds are
represented by their simplest or empirical formula, which simply shows the
relative number of atoms of each component and this smallest unit of ionic compounds
is called formula unit.
“Formula
mass of a substance (ionic compounds) is the sum of atomic masses of all atoms
in a formula unit shown by its simplest or empirical formula”.
The
relative formula mass (Mf) of an ionic compound is the relative
atomic masses (Ar) of all the atoms (ions) in its formula added
together.
The Mf of an ionic compound is equal to the mass in
grams of 1 mole of that compound.
Examples
Gram Atomic Mass (Gram Atom)
The relative atomic mass of an element expressed in gram
is called Gram Atomic Mass or Gram Atom. It is also called 1
mole. The one gram atom of all elements contains 6.02 x 1023
atoms.
1 gram atom = NA atoms = gram atomic mass
Examples
Gram Molecular Mass (Gram Molecule)
The relative molecular mass of a substance (element /
compound) expressed in gram is called Gram Molecular Mass or Gram Molecule.
It is
also called 1 mole. The one gram molecule of all
compounds contains 6.02 x 1023 molecules.
1 gram molecule = NA molecules = gram molecular mass
Examples
Gram Formula Mass (Gram Formula)
The relative formula mass of a ionic
compound expressed in gram is called Gram formula Mass or Gram formula. It is also called 1 mole.
The one gram formula of all ionic compounds contains 6.02
x 1023 formula units.
1 gram formula = 1 mole = NA formula units = gram formula mass
Examples
Gram Ionic Mass (Gram
Ion)
The relative ionic mass expressed in gram is called Gram ionic
Mass or Gram ion. It is also called 1 mole. The one
gram ion contains 6.02 x 1023 ions.
1 gram ion = 1 mole = NA ions = gram ionic mass
Examples
Molar Mass
General Definition
The relative atomic mass or molecular mass or formula mass of a substance expressed in gram is called its molar m
the mass in gram of 1 mole of units (such as atoms,
molecules or ions) of a substance is called its molar mass. The unit of molar
mass is gram or gram/mol.
Molar mass of Element
e.g.
the atomic
mass of carbon in gram is 12 g, so its molar mass would be 12 g.
Molar mass of covalent
compound
The molar mass of a covalent
compound (containing molecules) is its gram molecular mass which
is equal to the sum of the atomic masses of all the atoms comprising the
molecule.
e.g.
the gram molecular mass of H2O = 2 x1 + 1 x 16 =18 g, so its molar mass would be 18 g.
Molar mass of Ionic compound
The molar mass of an ionic compound
(containing formula units) is its gram formula mass, which is obtained by
adding the atomic masses of component ions.
e.g.
the
gram molecular mass of MgO = 1 x 24 + 1 x 16 = 40 g, so its molar mass would be
40 g.
Examples
Mole
General
Definition of Mole
Mole symbolized as mol is the S.I. base unit of chemical amount of substance. A mole of a substance can be defined as the atomic mass or molecular mass or formula mass of a substance (element or compound) expressed in gram containing 6.02 x 1023 particles (Atoms, molecules or ions).
OR
a mole is the gram atomic mass or gram
molecular mass for gram formula mass of any substance (i.e. element, covalent
compound and ionic compound), which contains Avogadro’s number (6.02 x 1023)
atoms, molecules or formula units.
One
mole of atoms or molecules or formula units of any substance will have a mass
in grams equal to the relative particle mass (Ar or Mm or Mf)
for that substance.
Examples
of Moles
1. Atomic
mass of Na is 23.0 amu, so 1 mole of Na is equal to 23.0 g (gram atom of Na)
2. Carbon has an Ar
of 12 amu, so one mole of carbon weighs exactly 12 g.
3. nitrogen (N2) gas has a Mf of 28
(2 x 14) amu, so one mole of nitrogen gas weighs exactly 28 g.
4.Molecular
mass of H2O is 18 amu, so 1 mole of H2O is equal to 18.0
g (gram molecule of H2O).
5 Hexane (C6H14) has a Mf of 86 [(6 x 12) + (14 x 1)] amu, so one mole of hexane weighs exactly 86 g.
6. Formula
mass of NaCl is 58.5 amu, so 1 mole of NaCl is equal to 58.5 g (gram formula of
NaCl).
The
mass (in g or kg) of 1 mole of units (such as atoms or molecules) of a
substance is called its molar mass with unit g-mol-1.
1 mole of anything = 6.02 x 1023 units
of that thing
1 mole of airline passengers = 6.02 x 1023 airline passengers
1 mole of compact discs = 6.02 x 1023 compact discs
S.I
Definition of Mole
A
mole is that amount of substance that contains as many number elementary
entities (particles or units) as there are atoms contained in exactly 12
g (0.012 kg) of the pure carbon-12 isotope.
Definition
of Mole in the light of
Avogadro’s number
In
the light of Avogadro’s number, mole is defined as the amount or mass in
gram of any substance which contains Avogadro’s number (6.02 x 1023)
of particles (atoms, molecules or ions).
Examples
Important Points of
Mole Concept
1. SI
base unit of amount of substance
2. Mole
provides information about number, mass and volume
Gram mole = mole
1 gram atom = 1
mole atom
1 gram molecule = 1 mole molecule
1 gram formula = 1 mole formula unit
1 gram ion =
1 mole ion
Importance
of mole
atoms, molecules and ions have very small
masses, so chemical experiments with measurable amount of substances involve an
enormous numbers of atoms, molecules and ions. Thus it is impossible to handle
and count atoms, molecules and ions individually. Therefore, chemists suggested
that it is convenient to group atoms, molecules and ions in a “Special Counting Unit” to measure chemical amount of substance and it is called a
Mole (abbreviated as mol, symbolized as n; from Latin moles meaning ‘heap or
pile’). Just as the unit ‘dozen’ refers to the number 12 and unit ‘gross,
refers to the number 144, the unit ‘mole’ refers to the number 6.02 x 1023
particles (this number is called Avogadro’s number donated as NA).
Thus
mole is a practical unit for handing atoms, molecules or ions. The mole concept
tries to give a practical meaning to the mass of reactants and products in
chemical reactions in terms of the number of particles (atoms, molecules, ions
or formula units) involved. A mole of substance always contains the same
number of particles irrespective of its state; solid, liquid or gaseous.
This actual countable number of particles is found out be 6.02 x 1023 that
is referred as Avogadro’s Number.
The gram is a
convenient mass unit because it matches human sizes. If we were a thousand
times greater in size (like Paul Bunyan) we would find it handy to use kilogram
amounts. This means the kilogram mole would be convenient. The number of
particles handled in a kilogram mole is 1000 times greater. The kilo
Avogadro number for the count of particles in a kilomole is 6.022 x 1026.
If humans were tiny creatures (like Lilliputians)
only 1/1000 our present size, milligrams would be more convenient. This
means the milligram mole would be more useful. The number of particles
handled in a milligram mole (millimole) would be 1/1000 times smaller.
The milli Avogadro number for the count of particles in a millimole is 6.022
x 1020.
Avogadro’s Number (NA)
Definition
A mole of substance always contains the same number of particles (atoms, molecules, ions or formula units), which is equal to 6.02 x 1023 (six hundred two thousand billion) irrespective of its chemical nature (element, covalent compound or ionic compound) or its state (solid, liquid or gaseous). This huge and constant number is called Avogadro’s number in the honour of Avogadro who gave chemistry a method for finding atomic and molecular masses.
“The number of elementary particles (atoms, molecules, ions or formula units) contained in one mole (i.e. gram atomic or gram molecular or gram formula mass) of a substance (element or compound) is found to be 6.02 x 1023 called Avogadro’s number or Avogadro’s constant. It is denoted as NA.” It is the number of particles per mole.
6.02 x 1023 particles = 1 mole of any substance
Number of particles means:
1. Atoms 2. Molecules 3. Formula units 4. Ions5. Electrons 6. Protons 7. Neutrons etc.
Derivation
Its value is derived by using the value of amu in gram as
Applications
Avogadro’s number is used to calculate:
1.The number of particles (atoms, molecules, ions or formula units) in a given sample of substance.
2.The mass of single atom or molecule of any substance in gram.
3. The mass of given collections of atoms or molecules of any substance.
Examples
Number of Particles in Different Moles
Loshmidt Number
The number of molecules per unit volume (i.e. one cubic centimeter) of an ideal gas at standard temperature and pressure (i.e. 0°C and a pressure of 1 atmosphere) is called Loshmidt Number denoted as N0, its value for 1 cubic centimeter being about 2.687 ×1019 cm-3. Its SI value is 2.6867811×1025 m−3
Molar Gas Volume or Molar Volume (VM)
The molar masses of most compounds are different. The
molar volumes of most solids and liquids compounds are also different. But the
molar volumes of gases (when measured at the same temperature and pressure) are
all the same i.e. if temperature and pressure stay the same, one mole of any
gas always has the same volume called molar gas volume. This strange
coincidence results from the fact that most of a gas is in fact empty space –
the molecules take up less than a thousandth of its volume at normal temperatures.
The volume of the molecules is negligible compared with the total volume, and
so any variation in their individual size will not affect the overall volume.
At room temperature (25°C, 298 K)
and standard pressure (1 atm, 1.013 x 105 Pa or 101.3 kPa) the molar
volume of any gas is 24.0 dm3 mol-1.
Definition
The space that one mole of a gas occupies at a certain temperature and pressure is known as molar gas volume i.e. It is the gas volume per mole at specified temperature and pressure.
It is the volume occupied by one mole of any gas at s.t.p or r.t.p. 22.4 dm3 (Litre) or 0.0224 m3 or 22400 cm3 (ml) of any gas at STP is referred to as Molar Volume. According to Avogadro’s Law, 22.4 dm3 of any gas at STP (273 K and 1 atm) constitutes its one mole (or molar mass).
The unit of molar volume is dm3 mol-1
(or cm3 mol-1 or m3 mol-1).
Molar Volume At STP
One mole of any gas at STP has a
volume of 22.4 dm3.
Molar Volume At RTP
One mole of any gas at RTP has a
volume of 24 dm3.
Factors Affecting Molar Volume
1. Molar volume is independent of the nature of the gas.
2. It
depends on temperature and pressure.
It is important when measuring molar volumes of gases always to quote the temperature and pressure as both affect volume. If the temperature increases, then so does the volume (Charle’s law). If the pressure increases, then the volume decreases (Boyle’s law).
In all
chemical calculations, molar gas volume will be measured at room temperature
and pressure (RTP or rtp) or
standard temperature and pressure (stp or STP). Room temperature is taken as 25°C (298 K) and room pressure as one
atmosphere (760 mm Hg).
Derivation of Molar Volume
In ideal gas equation; PV = nRT, the
ratio V/n is the molar volume which is equal to RT/P.
Different Values of molar volume for different moles
The value of molar volumes for different moles of any gas stp is given below:
STP/Standard temperature and pressure; ………………… 0°C or 273K and 1 atm
RTP/ Room temperature and pressure; …………………… 25°C or 298K and 1 atm
NTP/normal temperature and pressure; ………………....... 25°C or 298K and 1 atm
SATP = Standard Ambient temperature and pressure;…… 25°C or 298 K and 1 bar
(Ambient = environment or surrounding)