Avogadro’s Law/ Volume-Amount Law)
Introduction
and Statement
In 1811, an Italian physicist Amadeo
Avogadro advanced a brilliant hypothesis regarding the relationship between
the volume and amount (number of moles or number of molecules) of a gas
which was called Avogadro’s hypothesis and now it is called Avogadro’s
Law.
At constant
temperature and pressure, equal volumes of all gases contain the equal number
of molecules or moles i.e. the volume of a gas is directly proportional to the
number of moles (molecules) of the gas at constant temperature and pressure. In
other words, volume-amount (or mole) fraction i.e. volume-mole ratio of a gas
will always be the same if the temperature and pressure remain constant.
According to Law, 1 dm3 (1 cm3 or 1m3)
of oxygen contains same number of molecules as 1 dm3 (1 cm3
or 1 m3) of hydrogen or of any other gas, provided the volume are
measured under the same conditions. Stated differently, doubling the number of
moles of a gas doubles its volume, if temperature and pressure are constant.
This means that as long as the temperature and pressure remain constant, the
volume depends upon number of molecules of the gas or in other words amount of
the gas.
Another
Statement
Under the
similar conditions of temperature and pressure equal no. of moles (molecules)
will have equal volumes.
Examples
Avogadro’s Law in Everyday Life
1. A
flat tire takes up less space than an inflated tire.
2. Lungs
expand as they fill with air. Exhaling decreases the volume of the lungs.
3. A
balloon filled with helium weighs much less than an identical balloon filled
with air (since both balloons
contain the same number of molecules and since helium molecules have lower mass (4 amu) than either oxygen
molecule (32 amu) or nitrogen molecules (28 amu) in air, the helium balloon is lighter).
Mathematical
Expression For a Single Gas
Since equal number of molecules means equal
number of moles and thus the number of moles of any gas varies directly with
its volume, therefore:
V a n (at constant temperature and
pressure).
V = Kn [K is constant
of proportionality which depends upon pressure and temp]
V/n = K [V = k x N/NA, V = k x m/M]
V/n= K
It shows
that the ratio of volume to number of moles of a gas remains constant.
But
n = m/M
V = Km/M
OR
M = Km/V
M = K/d [so density of a gas is proportional to its molar mass)
The value of K is computed as:
K = V/n
But
V/n = RT/P [From,
PV = nRT]
K = V/n = RT/P
K = V/n = (0.0821 atmdm3mol−1K−1) x (273
K)/ (1 atm)
K = V/n =
22.4 dm3 mol-1
Thus k is found to equal to 22.4 dm3
mol-1 which is called molar volume or molar gas constant. The value
of k depends upon pressure and temperature and is independent of the nature
of the gas.
Mathematical
Expression for Two Gases
Suppose a
gas of n1 moles is enclosed in a vessel of V1 volume. If
we add more gas, the volume increases to V2, hence law can be
written as:
This is the second form of Avogadro’s law
Since both gases have same volume, V1
= V2
n2
= n1
And
Mathematical
Proof
Let us suppose that we have two gases A and
B whose number of moles are nA and nB respectively and
their volumes are VA and VB respectively; then
VA = KnA ––––––––––– (1)
VB = KnB ––––––––––– (2)
VA = VB
[According to
condition of Avogadro’s Law]
KnA = KnB
nA =
nB or MA/M.MA = MB/M.MB
It shows that equal volumes of gases contain
equal number of moles or molecules.
If on the other hand, equation (1) and (2)
are so equated that we have equal number of molecules in but the gases A and B,
then;
nA = nB
nA = VA/K
and
nB = VB/K
∴VA/K = VB/K
VA = VB
It shows that equal number of moles or
molecules of gases would occupy the same volume.
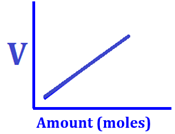
Graphical
Proof
The graph
between volume verses moles of a gas at stp is straight line indicating a
direct linear relationship between them.
Applications
and Information obtained from Avogadro’s Law
1. Determination of Relative Molecular
Mass of Gases
2. Molar Gas Volume/standard molar volume
3. Avogadro’s Number
4. Relation between Molar Volume, Mole and
Masses
1. Determination of Relative Molecular Mass of
Gases
Avogadro’s Law enables us to determine the
relative molecular mass of gases.
2. Molar Gas Volume/standard molar volume
The proportionality constant (k) of
Avogadro’s law shows that one mole any gas stp occupies 22.4 dm3 which
is referred to as molar volume or standard molar volume.
According to Avogadro’s Law, 22.4 dm3
of any gas at STP constitutes 1 mole of that gas. 22.4 dm3 or 0.0224
m3 or 22400 cm3 at STP is referred to as Molar Volume.
According to Avogadro’s Law, molar volume is independent of the nature of the
gas.
i.e.
1 mole of any gas at STP = 22.4 dm3
e.g.
1 mole of N2 gas at STP = 22.4 dm3
3. Avogadro’s Number
According to law, it is found that one mole
of any gas (and also one mole of all substances) contains the same number of
molecules called Avogadro’s number (NA) which is equal to 6.02 x 1023
e.g.
4. Relation between Molar Volume, Mole and
Masses
According to Avogadro’s Law, molar volume is
independent of the nature of the gas. Thus of any gas at stp constitute its
molar mass (mass in gram of one mole).Thus weight in gram of 22.4 dm3
of a gas at STP is the weight (mass) of one mole of that gas.
e.g.
1 mole of Cl2 gas = 71 g/mol = 6.02 x 1023 molecules
4. Relation between Molar Volume, Mole and
Masses
According to Avogadro’s Law, molar volume is
independent of the nature of the gas. Thus of any gas at stp constitute its
molar mass (mass in gram of one mole).Thus weight in gram of 22.4 dm3
of a gas at STP is the weight (mass) of one mole of that gas.
e.g.
volume of one mole of helium gas and neon
gas will be 22.4 dm3 although one mole of He gas is equal to 4 g and
that of Ne gas is equal to 20 g.