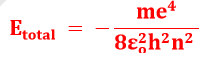XI Chemistry Test Model Questions for
Chapter # 2 (Atomic structure)
Short Questions-Answers
Q1.Write down short note on subatomic
particles.
Q2. Give 5 points of differences between:
(i) Alpha, beta and gamma rays
(ii) Continuous spectrum and Line Spectrum
(iii) Monochromatic and Polychromatic Light
Q3. Complete and balance the following
nuclear reactions:
Q4. What is quantum and photon? Write down main points of quantum
theory.
Q5. What
is radioactivity? How was this process discovered? Write down contribution of Marie
Currie and Pierre Currie. Describe an experiment to separate 3 types of nuclear
radiations.
Q6. What is spectrum and spectroscopy?
Define atomic emission and absorption spectrum. What is the importance of line
spectrum? Describe two types of line spectrum.
Q7. Write down 5 uses of nuclear radiations.
Q8. What is the Relationship between
Wavelength of X-rays and Nuclear Charge of Atom & how did Atomic Number
discover by Moseley?
Long Questions-Answers
Q9. What are X-rays? How are they produced? Give their properties, types
and uses. Describe role of X-rays in Moseley’s contribution.
Q10. What are the defects in Rutherford’s atomic model. State the
postulates of Bohr’s theory. How did Bohr’s theory explain the formation of the
line spectrum of hydrogen atom?
Q11. Write down Defects/ Limitations of Bohr’s theory or Bohr’s atomic
model
Q12. Write down 5 spectral lines of series of
atomic emission spectrum of hydrogen in tabular form with diagram. Write names
and formulae each series with their regions in electromagnetic spectrum.
Q13. Differentiate between Balmer Series and Lyman
Series. Explain hydrogen spectrum in
terms of Bohr’s theory
Q14. derive the formula for the radius and energy of nth orbit
of Hydrogen atom.
Q15. derive the formula for the energy of nth orbit of Hydrogen
atom.
Q16. Derive an expression for the frequency of radiation emitted from an
electron. Given that
Solutions
of Short Questions-Answers Test # 1
Q1. Write
down short note on subatomic particles.
Answer
Subatomic Particles
More than 100 subatomic particles have been discovered such as electron, proton,
neutron, positron, mesons, hyperons, neutrino, antineutrino, muon etc.
Fundamental particles
Out of 100 subatomic particles, only electron,
proton and neutron are considered to be fundamental particles of an atom as
they play an important role for the determination of physical and chemical properties
of element.
Almost all of the mass of an atom exists in nucleus
and nucleus was discovered by Rutherford (in 1911 A.D.). Except protium
(lightest isotope of hydrogen), nuclei of all other atoms contain neutrons.
Properties of Subatomic Particles
Electrons
Discovery -------- J.J.
Thomson in 1897 A.D (Crook’s discharge tube with perforated cathode)
Location -----------Orbits (100,000 times greater volume than nucleus but form less than one
percent total)
Charge -----------negative equal to positive charge of protons
Mass ------------nearly 1836 times less than proton and 1839 times less than
neutrons.
attractive Force -------- electrostatic force keeps electrons constantly moving around nucleus
Protons
Discovery ----------Goldstein
(1886 A.D) (cathode rays experiment, positive rays beam)
Location -----nucleus
Charge ------ positive equal to negative
charge of electrons
Mass ------------ nearly
1836 times than electron.
attractive Force ------Nuclear forces
Atomic Number -----No. of protons
Mass number ------ Sum
of no. of protons and neutrons
Neutrons
Discovery ------------ James
Chadwick (1932 A.D) (artificial radioactivity experiment, alpha-neutron
reaction of Be)
Location -----------------nucleus
Charge ------------------None or netural (not
deflected by electric or magnetic fields)
Mass ------------------- nearly 1836 times than electron (slightly heavier than protons)
attractive Force -------Nuclear forces (stability of nucleus depends upon the neutrons)
Atomic Number --------- No. of protons
Number
of neutrons ---Mass number–Number of protons
Q2.Give 5 points of differences between:
(i) Alpha, beta and gamma rays
(ii) Continuous spectrum and Line Spectrum
(iii) Monochromatic and Polychromatic Light
Distinction between Alpha, beta and gamma
rays
Distinction between Continuous and Line Spectrum
Distinction between Monochromatic and
Polychromatic Light
Q3. Complete and
balance the following nuclear reactions:
Q4. What
is quantum and photon? Write down main points of quantum theory.
Quantum
The emission or absorption of energy
(light) occurs in small packets of energy or specified amount called quanta
which is defined as the smallest unit of radiation energy which can exist
independently.
Photon
A quantum of radiant energy in the form of light is called
Photon.
Basic Postulates of PQT
This theory explains the nature of light
in terms of Quanta which is the smallest unit of radiation energy.
1.Atoms cannot absorb or emit energy continuously.
2. The emission or absorption of energy (light) occurs in small packets of energy called quanta.
3. The amount of energy of quantum is directly proportional to the frequency of the radiations emitted or absorbed by the body. i.e.
E 𝛂 u or E = hu (This is called as Planck’s equation)
Where,
E = Energy gained or lost by body.
h = Planck’s constant =
6.625 x 10–34 J.s (6.625 x 10–27 Ergs.sec).
u =
Frequency of radiation
Q5. What
is radioactivity? How was this process discovered? Write down contribution of
Marie Currie and Pierre Currie. Describe an experiment to separate 3 types of
nuclear radiations.
Definition
Radioactivity is the nuclear phenomenon
in which there is a spontaneous and continuous emission of nuclear radiations
from atom whose atomic number is greater than 83 due to the splitting of atomic
nuclei.
Discovery and First Radioactive element discovered
The phenomenon of radioactivity was
discovered by a French professor, Henry Becquerel in 1896 A.D. while working on
uranium mineral called Pitch-blende (an oxide of uranium; U3O8).
He observed that there was continuous emission of some invisible radiations
which producing bright spots on (fogging) photographic plates, ionizing gases,
penetrating through thin metal sheets and producing fluorescence on zinc
sulphide screen. This process of emitting invisible radiations was termed as
radioactivity.
Discovery polonium and radium By Marie Currie and Pierre Currie
Marie Currie and her husband, Pierre Currie isolated the radioactive
component of the pitch blend mineral and separated two new radioactive elements
polonium and radium.
Experiment
for Separation and Detection of Radiation
To study the nature of radiations,
Rutherford placed a small piece of radioactive material is in a Lead Block
having a small hole in it. The radiations emitted by radioactive substance were
passed through an electric field. (In fact, they are first subjected to pass
through a vacuum chamber with a photographic plate in which a magnetic or
electric field is applied).
Derivation of Radius of the nth Bohr’s Orbit for Hydrogen-Like Atoms
Assumptions for Simple Atom
To derive an expression for radius, consider a hydrogen atom (or hydrogen-like atoms such as He+, Li2+, Be3+, B4+, C5+) with atomic number equal to Z consisting of a single electron with charge –e and mass m revolving around the nucleus of charge +Ze (+e is charge of proton) with a tangential velocity v in the orbit whose radius is r.
Now revolving electron is being acted upon simultaneously by the following two types of forces;
(i) Electrostatic force of Attraction / Centripetal Force
According to Coulomb’s law, the electrostatic force of attraction (Fe) between the nucleus of charge ‘+Ze’ and electron of charge ‘–e’ separated by a distance ‘r’ is given by:
Where ‘K’ is proportionality constant. It is equal to 1/4πεor2
Hence attractive force between nucleus and electron can be written as
(ii) Centrifugal Force
This Coulombic force of (Fc) supplies the centrifugal force to keep the electron in an orbit and is given by:
Equating Fe and Fc
To keep the electron in the same orbit, these two opposite forces must be equal to each other i.e.
Determination of v2 of electron by using Bohr’s Postulate
According to Bohr’s postulate, angular momentum of electron revolving around the nucleus is an integral multiple of h/2p.
Calculation of Radius (r)
Substituting the value v2 from equation (ii) in equation (i)
Where
h = Planck’s constant = 6.625 x 10−34 J.s
me = Mass of electron = 9.11 x 10−31 kg
e = Charge of electron = 1.602 x 10−19 C
𝛆o = Vacuum permittivity constant = 8.84 x 10−12 C2/J.m
Calculation of nth Bohr’s orbit (rn)
Assembling all constants in equation (iii), we get
Where a is known as Bohr’s constant or Bohr radius and its value is 0.529 x 10−8 cm or 0.529 Å or 0.0529nm or 52.9 pm. This is the radius of the first orbit of H. This equation is used for the determination of nth orbit of hydrogen atom and hydrogen like ions like He+, Li2+ etc.
The above equation shows that radius of orbit is directly proportional to the square of the principal quantum numbers (r α n2 i.e. 1, 2, 3, ……..) and inversely proportional to atomic number. As the value of n increases, the radius of the orbit will increase.
Derivation of Energy of the nth Bohr’s Orbit
Basic of Derivation
The total energy of an electron revolving in any orbit around the nucleus is the sum of kinetic energy and potential energy given by,
Etotal = K.E + PE ……………….(i)
Calculation of K.E
The K.E. of electron with mass m revolving around the nucleus with velocity v is given by the following expression;
Now the centrifugal and centripetal forces upon the revolving electron are given as:
At uniform circular equilibrium motion, these two opposite forces must be equal to each other i.e.
Calculation of P.E.
P.E is the work done in bringing the electron from infinity to a point at a distance r from nucleus and can be calculate as
P.E =work done = −force x displacement = −Fe x r
Here negative sign indicates that P.E decreases when electron is brought form infinity to a point at a distance r. Here negative sign indicates a net attractive interaction, giving algebraically lower energy at shorter distance.
Calculation of Total Energy
Etotal = K.E + PE
Here K is a factor assembled by various constant present in energy equation. Its value is 2.18 x 10−18 J/atom or 1312.8 kJ/mol
E is always negative. Negative sign shows that the electron is bound to the atom and energy must be spent in order to remove it from the orbit.
All energy states are bound states as the negative sign indicates. When n = 1; this corresponds to electron at the closest possible distance from the nucleus and at its lowest energy and is called ground state energy. All energy states with value of n higher than 1 are termed as excited states. When n = α then E = 0; which means that the system is unbound and the electron is free.
It should be noted that the energy is increasing as the n (orbits) increasing; however the difference of energy between two orbits is decreasing.
Conclusion
If total energy = − x
Then
KE = + x
PE = − 2x
2.12 Expression for ∆E of Electronic Transition between Orbits
Calculation of ∆E
Let E1 be the energy of n1 orbit and E2 is for n2 orbit. To calculate the energy emitted by atom in the form of radiation when an electron jumps from a higher energy state n2 to lower energy orbit n1; let us make use of the postulate of Bohr’s model; according to which, the emitted energy is written as
Emitted energy = ∆E = E2 – E1
But,
This equation is used for determining the emission or absorption of energy when electron jumps from one orbit to another
2.13 Expression for Frequency of Electronic Transition between Orbits
Calculation of ∆E
Let E1 be the energy of n1 orbit and E2 is for n2 orbit. To calculate the energy emitted by atom in the form of radiation when an electron jumps from a higher energy state n2 to lower energy orbit n1; let us make use of the postulate of Bohr’s model; according to which, the emitted energy is written as
Emitted energy = ∆E = E2 – E1
But,
To calculate the frequency (u) of emitted radiations (or photons there in); let us make use of the Bohr’s postulate; according to which:
hu = ∆E = E2 – E1
But
To calculate the frequency (u) of emitted radiations (or photons there in); let us make use of the Bohr’s postulate; according to which:
hu = ∆E = E2 – E1
But
Expression for Wave Number and Wave Length of Radiation
Q1. Differentiate between Orbit and Orbital
Q2. What are quantum numbers? Give a brief account of 4 quantum
numbers. Write all possible value of l, m and s
for n=2 and n=3
Q3.Write down the four Quantum numbers of both electrons of
Helium atom.
Q4. State and illustrate the following rules of electronic configuration
(i) Pauli Exclusion principle
(ii) Hund’s rule of maximum multiplicity
Q5.Write down the Electronic Configuration of Boron and Carbon
atom in ground state and excited state
Q6. Draw shapes of orbitals for third energy level (l=0, l=1,
l=2) (s, p and d-orbitals).
Q7.Arrange the following energy levels in ascending order
using (n+l) rule: 5d, 3s, 4f, 7s, 6p, 2p
Q8. Write down the E.C. of S, Na+, Cl−, Cr, Fe, Cu, Ag, Mo, Br−, I, P3−, S2−, C4−, Cu+, Sr2+, Ca2+, Mg2+, Al3+, Fe2+, Fe3+
(i) S (Z = 16) = 1s2, 2s2, 2p6, 3s2, 3p4
(No. of electrons in S (atom) = Z =16)
(ii) Na+ (Z =11)= 1s2, 2s2, 2p6
(No. of electrons in Na+ (cation) = Z – charge = 11 – 1 = 10)
(iii) Cl− (Z = 17)= 1s2, 2s2, 2p6, 3s2, 3p6
(No. of electrons in Cl− (anion) = Z + charge = 17+ 1 = 18)
Q9. Which rule and principle is violated in writing the following E.C.
i) 1s2, 2s3 (Pauli’s exclusion principle; 1s2, 2s2 2px1)
ii) 1s2, 2px2 (Aufbau principle; 1s2, 2s2)
iii) 1s2, 2s2, 2px2 2py1 (Hund’s rule; 1s2, 2s2 2px1 2py1 2py1)
iv) 1s2, 2s2 2p6, 3s2 3p6, 3d4 4s3 (Pauli’s exclusion principle and Hund’s rule; 1s2, 2s2 2p6, 3s2 3p6, 3d5 4s1 )
Q10. Identify the orbital of higher energy in the following pairs
(i) 4s and 3d (3d >4s)
(ii) 4f and 6p (6p>4f)
(iii) 5p and 6s (6s>5p)
(iv) 4d and 4f (4f>4d)
Q11. Explain why
the filling of electron is 4s orbital takes place prior to 3d?