Uncertainty in Measurement
1. Any measurement is only as good as the “skill of the person” doing the work and the “reliability of the equipment used”. In scientific work, we recognize two kinds of numbers; exact numbers and inexact numbers.
2. Exact numbers are those that are known with exactly or are integers that result from counting numbers of objects. For example; by definition there are exactly 12 eggs in a dozen, exactly 1000 g in a kilogram and exactly 2.54 cm in an inch.
3. Inexact numbers are those whose values have same uncertainty. Numbers obtained by measurement are always inexact i.e. uncertainties always exist in measured quantities. This is due to inherent limitations in the equipment used to measure quantities (equipment error) and there are differences in how different peoples make the same measurement (human error).
4. Every physical measurement involves error and every physical measurement is an approximation. The terms precision and accuracy relate to how good an approximation is. We usually think of precision and accuracy as pretty much the same thing. But in science, these words are used in significantly different meanings. Similarly, the margin of error in a measurement is reflected by the number of significant figures in a measured quantity.
All measurements of physical quantities are subject to uncertainties in the measurements. Variability in the results of repeated measurements arises because variables that can affect the measurement result are impossible to hold constant. Even if the "circumstances," could be precisely controlled, the result would still have an error associated with it. This is because the scale was manufactured with a certain level of quality, it is often difficult to read the scale perfectly, fractional estimations between scale marking may be made and etc. Of course, steps can be taken to limit the amount of uncertainty but it is always there.
In order to interpret data correctly and draw valid conclusions the uncertainty must be indicated and dealt with properly. For the result of a measurement to have clear meaning, the value cannot consist of the measured value alone. An indication of how precise and accurate the result is must also be included.
Thus, the result of any physical
measurement has two essential components:
(1) A
numerical value (in a specified system of units) giving the best estimate
possible of the quantity measured,
and
(2) the degree of uncertainty associated with this estimated value.
Uncertainty is a parameter characterizing the range of values within which the value of the measurand can be said to lie within a specified level of confidence.
For example, a measurement of the width of a table might yield a result such as 95.3 +/- 0.1 cm. This result is basically communicating that the person making the measurement believe the value to be closest to 95.3cm but it could have been 95.2 or 95.4 cm. The uncertainty is a quantitative indication of the quality of the result. It gives an answer to the question, "how well does the result represent the value of the quantity being measured?"
Significant Figures/Significant Digits
Definition
It is often impossible to obtain the
exact value of the quantity under investigation. The numerical value of every
observed measurement is an approximation. No physical measurement (such as length,
mass, time, volume etc) is ever absolutely correct. The accuracy
(reliability) of every measurement is limited by the reliability of the measuring
instrument, which is never absolutely reliable. The
number of significant figures indicates margin of error in a measurement. A significant
figure is one which is known to be reasonably reliable. In elementary
measurements in chemistry and physics, the last digit is estimated and is also
considered as a significant figure i.e. when significant figures are
counted, the last digit is understood to be
uncertain. the term digit denotes any one of the ten numerals, including zero.
The Statistically
Significant digits or Meaningful
or Reliable digits of a number known with
certainty in a measured (calculated) quantity which are needed to express the precision of the measurement are known as significant figures. The certain digits of a
measured quantity plus one
uncertain rightmost last digit are counted
as significant figures.
OR
The number
of digits in a measurement about which we are reasonably sure are called
significant figures. They help us to know about the extent of uncertainty in
the measurement.
The number
of significant digits depends on the least count of the instrument use. But it
does not depend on the system of units used.
Significant figures are those meaningful digits that are known with certainty. They indicate uncertainty in an experiment or calculated value. For example, if 15.6 mL is the result of an experiment, then 15 is certain while 6 is uncertain, and the total number of significant figures are 3. Hence, significant figures are defined as the total number of digits in a number including the last digit that represents the uncertainty of the result.
Significance
The number of significant figures is
directly related to the precision and accuracy of
measurements that are made in scientific work.
Greater the number of significant figures in a quantity, greater the certainty and precision in that quantity. The measured quantity with greater significant figures is more precise than quantity having less significant figure. Hence less significant figure means low precision.
Rule of most Significant Digits & Least Significant Digits
1. The
left most non-zero digit is the most significant digit.
e.g.
(i) The digits 5 is the most significant
digit in number 59832
(ii) The digits 4 is the most significant digit in number 0.00476320
2. If there is no decimal point, the right most non-zero digit is the least significant digit.
3. If
there is decimal point, the right most digit, whether zero or non-zero, is the
least significant digit.
e.g.
(i) 3567.2 → 2 is the least significant
digit
(ii) 83.560 → 0 is the least significant
digit
4. All digits including most and least significant digits are significant figures.
Summary of Guideline Rules for determining the significant figures
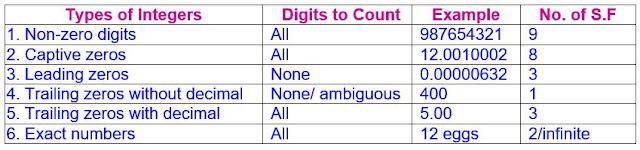
1. Non-zero digits (any digit that is not zero i.e. 1-9 integers) are all significant.
2. Captive Zeros (i.e. zeros placed between two non-zero digits) always count as significant.
4. Trailing zeros (i.e. zeros at the right end of the number) right of decimal point are always significant
5. Trailing zeros in numbers with no decimal point are not significant Zeros
Guideline Rules for determining the Significant Figures
1. non-zero digits (any digit that is not zero i.e. 1-9 integers) are all significant.
e.g.(ii) 435 kg has three significant figures.
2. Captive Zeros (i.e. zeros
placed between two non-zero digits) always count as significant.
(i.e. zeros in the middle of a number are always significant. All zeros becomes significant if they appears between two non-zero digits)
e.g.(i) 4090 mg → has three significant figures.
(ii) 28.073 g → has five significant figures.
(iii) 6004 kg → 4 significant figures
(iv) 43200209 mg → 8 significant figures
3. Leading
Zeros (i.e. zeros precede the nonzero digits) are not significant.
(i.e. zeros at the beginning of a number to the left of the first non-zero digit relating to the value less than one are non-significant. Such zeroes merely indicate the position of the decimal point)
e.g.
(i) 0.0006 nm → has 1 significant figures.
(ii) 0.00027 mm → has 2 significant figures.
4. Trailing zeros (i.e. zeros at the right end of the number) right of
decimal point are always significant
(i.e. Terminal or Final zeros to the right of the decimal point in a number less than or greater than one are significant. The assumption is that these zeros would not be shown unless they were significant.) e.g. 55.220 has 5 significant figures (If the value were known to have only 4 significant figures, we would write 55.22). Similarly, 0.21000 has 5 significant figures.
e.g.(i) 3.00 m has three significant figures.
(ii) 5.900 kg has four significant figures.
5. Trailing zeros in numbers with no decimal point are not significant Zeros
e.g.(i) 140 miles → has 2 significant figures.
(ii) 786000 cal → has 3 significant figures.
Correct Rule
zeros at the
end of a number and before the decimal point relating to the value greater than
one i.e. trailing zeros left of the decimal point are ambiguous and are not
necessarily significant. They may or may not be significant.
e.g.
(i) 5200
miles may have 2, 3 or 4 significant figures (but we cannot tell from the way
is written. It is very poor form to
report numbers with an ambiguous degree of uncertainty).
(ii)50,600 calories may have 3,4 or 5 significant figures.
This potential ambiguity can be avoided
by using standard exponential or scientific notation.
For example,
Depending upon whether the number of
significant figures is 2,3 or 4, we would write 5200 calories as
5.2 x 103 calories (2
significant figures)
5.20 x 103 calories (3 significant
figures)
5.200 x 103 calories (4 significant figures)
6. Exact numbers i.e. “Counts” and “Defined numbers” have infinite number of significant digits. They have no uncertain digits and they can be assumed to have an infinite number of significant figures and all digits in them are counted as significant. Exact numbers are of two types:
(a) Cardinal Numbers (Counting numbers); are exact by definition.
e.g.A dozen of egg contains exactly 12 eggs, not 12.000001 eggs. Eggs only come in whole numbers.
(b) Constants or Mathematical relationships; are exact by definition.
e.g.
7. All zeros of the
right of left or both side of non-zero digits are not significant.
0056 → 2 significant
figures
3800 → 2 significant
figures
002800 → 2 significant
figures
0802900 → 4 significant figures
8. In exponential
notation, the numerical portion or coefficient number gives the number of
significant figures.
e.g.
2.45 x 10-3
→ 3 significant figures
4.030 x 104 → 4 significant figures
Explanation of Rule # 1 …. Non-zero Digits are always significant
If we measure something by using a device (like ruler, thermometer, triple beam balance etc.), we get a number, then we have made a measurement decision and act of measuring gives significance to that particular numeral or digit in the overall value we obtain. Hence a number like 58.97 g would have four significant figures and 3.64 m would have three. (The problem comes with numbers like o.0008740 or 45.002.
Explanation of Rule # 2 …. Captive or Captured zeros are always significant
Any zeros between two significant digits are significant. These zeroes are sometimes called captured zeroes.
Suppose you had a number like 406. By the first rule, the 4 and the 6 are significant. However, to make a measurement decision on the 4 (in the hundred’s place) and the 6 (in the unit’s place), you had to have made a decision on the ten’s place. The scale for this number would have hundreds and tens marked with estimation made in the unit’s place. Like this,
Explanation of Rule # 3, 4…. A final or trailing zeros in the
decimal portion only are significant.
0.00500
0.03040
2.30 x 10-5
4.500 x 1012
Use of significant
digits in addition and subtraction
The result of addition or subtraction must carry the same number of digits to the right of the decimal as any of the original number with fewest digits to the right of the decimal. (i.e. the result has the same number of decimal places as the term having smallest number of decimal places or the least precise measurement used in the calculation). This means that only as many digits are to be retained to the right of the decimal point in the answer as the number with fewest digits to the right of the decimal.
Note for
addition and subtraction, the decimal places are counted.
e.g.
5.3 + 7.24 = 12.5 (but not 12.54)
16.72 – 6.5 = 10.2 (but not 10.22)
Example # 1: Let us add 15.020, 9986.0 and 3.518
The result should be rounded off to
one decimal place because 9986.0 has smallest number of decimal place (only
one).
Example # 2: Let us add 12.12, 18.0 & 1.014
Use of significant
digits in multiplication and division
The result of multiplication and division cannot have more significant figures than the least precise term of known quantity in the calculation (i.e. the number of significant figures in the final product or quotient contains the same number of significant figures as the original number with the fewest significant figures called least precise factor; LPF). This means that number obtained as a result of multiplication or division of two or more numbers must have no more significant figures than the least number of significant figures in any of the multiplied or divided term.
Note that for multiplication and
division, significant figures are counted.
Example #1: Solve 1.32 x 4.421
1.32 (3 significant figures) x 4.421 (5 significant figures)
= 5.83572 (Not according to rule)
= 5.84 (3 significant figures)
The result is rounded off to three significant figures because least precise factor is 1.32 which has 3 significant figures.
Exponential Notation/ Scientific Notation
Definition
The short
hand expression of a very large or a very small number by means of exponents is called exponential
notation or scientific notation.
OR
Scientific
notation is a product of co-efficient number (digit term) and 10 raised to
some power (exponential term).
OR
In Scientific
notation, numbers are written as a product of two terms, the first is a decimal
part called co-efficient number (digit term) and the second is 10 raised to a
suitable power called exponential term.
Co-efficient is the number between 1 to 10 that is multiplied by 10 raised to a power. The powers to the base 10 are known as exponents which may be positive, negative or zero while integer power of 10 is called exponential notation.
e.g.
602,000,000,000,000,000,000,00 representing
Avogadro’s Number, is more conveniently written in Exponential Notation as 6.02
x 1023
General Representation
In exponential notation, the numbers are expressed as X x 10±y ;
 |
| Exponential Notation |
X = Co-efficient No. or digit term ranges 1 to 10
10 = Base
y = Positive or negative integer called Exponent Power
Standard Scientific Notation
Standard Scientific Notation is one in which decimal point is after one digit of co-efficient number.
For example
4.56 x 106 is a
standard scientific notation while 45.6 x 105 is not a standard
scientific notation”.
Rules for determination of numerical
value of exponents
The numerical value of exponents is
determined by following Rules:
Rule I for determination of numerical
value of exponents
Exponent is positive, when
decimal point is shifted towards left. The exponent is numerically
equal to the number of places the decimal point has been moved. The
numbers which are greater than one have positive exponents. Such
notations may be represented by a general formula 10n where n
is the number of zeros. e.g.
Rule II for determination of Numerical Value of Exponents
Exponent is negative, when decimal point is shifted to right. The exponent is equal numerically to the number of places the decimal point has been moved. The numbers which are less than one have negative exponents. Such notations may be represented by a general formula 10n+1 where n is the number of zeros. e.g.

1. Minimization of Errors
2. Time Saving
3. Memorization of values of constants
4. Indication of Significant Digits
5. Simple and Easy Calculation
Rounding Off Data/Lumping
Definition
Rounding means reducing the
digits in a number while trying to keep its value similar. The result is
less accurate, but easier to use.
To round
off means to reduce a number to the desired significant figures. It is the
procedure of dropping non-significant digits in a calculation and
adjusting the last digit reported. Thus dropping off last digit of a data to
reduce a number to the required significant digit is called Rounding Off
Data.
OR
It is an operation of dropping insignificant digits from the numbers used in expressing a quantity”.
Correcting a physical quaintly by dropping the last digits which are insignificant and are beyond the precision of the measurement is called rounding off or Lumping
Rounding off a decimal is a
technique used to estimate or approximate values. Rounding is most commonly
used to limit the amount of decimal places. Instead of having a long string of
decimals places, or even one that goes on forever, we can approximate the value
of the decimal to a specified decimal place.
We can round to any place. After
rounding, the digit in the place we are rounding will either stay the same,
referred to as rounding down, or increase by 1, referred to as rounding up.
Rules for Rounding Off Data
1. If last dropping digit is greater than five, then the last remaining digit to be retained is increased by one unit. This is called rounding up.
(Rounding up means that we increase the terminating digit by a value of 1 and drop off the digits to the right. If the next place beyond where we are terminating the decimal is greater than or equal to five, we round up. For example, if we round 5.47 to the tenths place, it can be can be rounded up to 5.5).
e.g.
2. If last dropping digit is less than five, then the last remaining digit will remain unchanged. This is called rounding down.
(If the number to the right of our
terminating decimal place is four or less (4, 3, 2, 1, 0), we round down. This
is done by leaving our last decimal place as it is given and discarding all
digits to its right. For example, if we round 6.734 to the hundredths
place, it can be rounded down to 6.73).
e.g.
5.734 is rounded off to 5.73 to 3 significant digits.
5.734 is rounded off to 5.7 to 2 significant digits.
73
rounded down to the nearest ten is 70, because 73 is closer to 70 than to 80.
3. If
last dropping digit is exactly five, then the
last remaining digit is increased by one unit if it
is odd and remain unchanged if it is even e.g.
7.865 is rounded off to 7.86 to 3 significant digits [L.R.D. = even]
8.775 is rounded off to 8.78 to 3 significant digits [L.R.D. = odd]
How to Round Numbers
1. Decide
which is the last digit to keep
2. Leave
it the same if the next digit is less than 5 (this is called rounding down)
3.But
increase it by 1 if the next digit is 5 or more (this is called rounding up)
Example
74 gets
"rounded down" to the nearest 10 is 70)
We want to keep the "7" as
it is in the 10s position. The next digit is "4" which is less than
5, so no change is needed to "7"
Example
86 gets
"rounded up" to the nearest 10 is 90
We want to keep the "8". The
next digit is "6" which is 5 or more, so increase the "8"
by 1 to "9"
Precision
1. Think of
precision as the consistency of measurements.
Precision is the concordance of a series
of measurements of the same quantity i.e. precision refers to the degree of
closeness (agreement) and uniformity (reproducibility) in a collection
experimental results (based upon some accepted standard of closeness generally
called a percentage error) of the same value (and is estimated by repeating the
measurement under same conditions as nearly identical as possible). Thus
precision expresses the close reproducibility or close
agreement of several results of measurement.
Precision is a measure of how closely individual measurements of the same quantity agree with one another. The precision of a measurement system, related to reproducibility and repeatability, is the degree to which repeated measurements under unchanged conditions show the same results
Precision is an indicator of the scatter in the data. The lesser the scatter, higher the precision.
2. Precision relates to the quality
of an operation by which a result is obtained. Thus, precision shows the degree of
refinement in the performance of an operation i.e. precision of a result is an
indication of how sharply it is defined. Precision is the measure of degree of
perfection in the instruments and methods used to obtain a result.
3. If measured results are close to each other then precision is high and vice versa. The precision of the measurement is an indication of how close multiple measurements would be expected to agree with one another. A precise work is done carefully and result achieved by precise work is more likely to be common or same.
4. Poor precision results from poor technique.
5. Poor precision is associated with random error i.e. lack of precision gives rise to random error.
6. Precision is checked by repeating measurements. It is calculated by arithmetic method.
7. It depends upon least count of the measuring equipment.
8. In general, the more
precise a measurement, the more accurate it will be.
i.e. precision always accompanies accuracy but a high
degree of precision does not imply
accuracy. Thus it is possible for a precise value to be inaccurate.
For example, an improperly calibrated meter stick or a faulty but very sensitive balance may give precise readings that are in error (i.e. inaccurate). Thus good precision is usually a sign of good accuracy but precision does not guarantee accuracy.
9. The precision of a measurement describes the units used to measure something. (e.g. you might describe your height as “about 6 feet”. That wouldn’t be very precise. If however you said that you were “74 inches tall”, that would be more precise. Thus the precision of a measurement depends on the size of the smallest measuring unit. [Sometimes in real life we don’t want to be precise. This is probably because less precise results are easier to remember].
10.It is impossible to make a perfectly
precise measurement. Since there is no limit to the tiny size of the unit you can
measure with (as long as you can afford and expensive instrument), there is no
limit to how precisely you can measure a quantity. To obtain a higher degree of
precision, it may be necessary to use more sophisticated (costly) equipment or
a more time-consuming methodology.
11.In quantitative analysis,
the precision of measurement rarely exceeds 1 to 2 parts per thousand (0.1 to
0.2 %). The mean deviation (error) or relative mean deviation is a measure of precision.
12. The analogy of darts stuck in a dartboard pictured in figure illustrates the difference between the two terms:
A measurement system can be accurate
but not precise, precise but not accurate, neither, or both. For example, if an
experiment contains a systematic error, then
increasing the sample
size generally increases precision but does not improve accuracy.
The result would be a consistent yet inaccurate string of results from the
flawed experiment. Eliminating the systematic error improves accuracy but does
not change precision.
Accuracy
1.Think of accuracy as the “trustworthiness” or "trueness" of a
measurement.
Accuracy is the concordance between measured
result and the true or most probable value i.e.
accuracy refers to the degree of conformity (nearness
or orthodoxy) with a standard accepted value. Thus accuracy expresses the close
reproducibility or close agreement of measured result with true or universally
accepted result.
Accuracy is a measure of how closely individual measurements of the same quantity agree with true result (which need to be very precise and universally accepted). Thus, accuracy shows the degree of correctness or exactness of a measurement. Accuracy expresses the external consistence or agreement of a measurement when compared to an authoritative or expert value.
2. Accuracy relates to the quality of results.
3. If measured results are close to true value then accuracy is high and vice versa. Accuracy shows how closely the measured results agree with correct value.
4.Poor accuracy results from procedural or equipment flaws
5.Poor accuracy is associated with systematic error i.e. lack of accuracy gives rise to systematic error.
6.accuracy is checked by using a different method. It is calculated by Statistical method
7.It is independent of the least count of the measuring equipment,
8. It is a common misconception (fallacy) that good precision means good accuracy but it is not always true. The result of precise work is not coincide with true or accurate result due to faulty apparatus. In that case work is precise due to close agreement of several measured result but it is not accurate because of faulty equipments. Thus accuracy requires precision but precision does not guarantee accuracy as a precise work may also be inaccurate due to a faulty apparatus.
9. The accuracy of
measurement is independent of the size of the measuring unit.
Difference between Precision and Accuracy
Error and its Types
Definition of Deviation
The difference between measured results with each other i.e. the departure of measured results from each other is called deviation
Definition of Error
Chemistry is an experimental science in which every quantitative measurement is subjected to some degree of uncertainties. This is due to inherent limitations in the equipment used to measure quantities (Equipment error or random error) and there are differences in how different peoples make the same measurement (human error or systematic error). Thus, measurement by its nature, is inexact, the magnitude of that “inexactness” is the error.
The difference between measured (or observed)
result and the true (most probable) result is called Error. i.e. the departure
of a measured result from factual result is called error. The uncertainty in
measurement is called error.
Error
= True value – measured value
We try to reduce error by carrying
out additional measurements or by changing our experimental apparatus, but we
can never eliminate error altogether. Thus, error is inherent in measurement.
Causes of Errors and Deviations
Errors and deviations in repeated measurements are due to following two factors:
1. Fundamental inadequacy or defect in the instrument (gives rise to Random errors)
2. Lack in handling the apparatus & Improper functioning of the equipment (gives rise to Systematic errors)
|
|
Classification of Errors
Errors in analysis may be classified as1. Determinate/ Systematic/ Avoidable Errors (Due to lack of accuracy)
2. Random/ Indeterminate/ Unavoidable Errors (Due to lack of precision)
Difference between Systematic and Random Errors
1. Systematic
Errors/ Determinate Errors
1. Systematic errors are
caused by the defect in the analytical method or by the improper
functioning of instrument. Such systematic errors may result from mis-calibration
of the experimental apparatus or from a fundamental
inadequacy in the technique for measuring a quantity.
OR
The errors which
appears in a measurement due to known causes is called systematic error.
2. Systematic errors are reproducible
inaccuracies that are consistently in the same direction (either
positive or negative) that limit accuracy of results. They
always affect the measurement in the same way; no matter how many times the
measurement is made. Systematic errors are often due to a problem which
persists throughout the entire experiment.
3. Systematic errors are avoidable (correctable
or preventable) because the cause of error may be eliminated or corrected.
For Example, in
volumetric titrations an improperly prepared indicator will give colour change
prior to (before) the equivalence or end point, thereby producing systematic
error.
Similarly if burette
is not properly cleaned or rinsed, then it will cause a systematic error.
4. The repetitions
of the same measurement neither reveal nor remove systematic errors i.e. Repeating
the measurement a number of times will have no effect on this type of error.
If a Systematic error
is known, we should do our best to correct for it before reporting the result
the result.
For example; if our
apparatus has not been calibrated correctly, it should be recalibrated.
One thing you can do to reduce such errors is to take Pilot Test of your measurements.
5. They limit accuracy of result.
6. Systematic errors are much more problematic as they are difficult to detect and cannot be analyzed statistically (thereby reducing accuracy of result) because all of the data is off in the same direction (either too high or too low).
For example; the
cloth tap that you use to measure the length of an object had been stretched
out from years use. As a result, all of your length measurements were too
small.
Similarly the
electronic scale you use reads 0.05 g too high for all your mass measurements
because it is improperly tarred throughout your experiment.
7. Systematic errors are constant and always of the same sign and thus may not be reduced by averaging over a lot of data.
8. Generally speaking,
systematic errors are hard to identify with a single experiment.
Sources of Systematic Errors
1. Instrument errors (Incorrect
design or improperly calibrated instrument)
2. personal errors (Incorrect reading or misreading and
interpretation of a measuring device)
3. Imperfections in
experimental techniques or procedure (Lack of accuracy of the formula used)
Minimization of Systematic errors
1. By improving experimental
techniques
2. Selecting better instruments
3. Removing personal bias
Examples of systematic errors
(i) time measurements by a clock that runs too fast or slow,
(ii) distance measurements by an inaccurately marked meter stick
(iii) current measurements by inaccurately calibrated ammeters, etc.
(iv) calibration error
(v) Parallax error
2. Random
Errors/ Indeterminate Errors
1. Random errors are
caused by the fundamental inadequacy in the instrument or by the uncertainty
in every physical measurement as there are always inherent
limitations in the equipment used to measure quantities.
OR
The
error which appears in a measurement due to unknown causes is called random
error.
2. Random errors are statistical fluctuations (in either direction) in the measured data that affect precision of the result. These errors are due to poor equipment and to carelessness in making proper observations. They as often give a result that is too high as they do one that is too low. That is why they may be positive or negative (i.e. it tends to be up or down randomly). That is why the average of several replicate measurements is taken which is more reliable than any individual measurement.
3. Random errors are unavoidable (in-correctable
or inescapable or unpreventable) as the cause of such errors cannot be
eliminated.
For Example; In a 50 ml burette, we can read the burette reading accurately only to the nearest 0.1 ml which gives rise to random errors.
4. Repeating a measurement many times reveals the magnitude of the random errors. Thus the average of several replicate measurements is taken to reduce and eliminate random errors thereby improving the precision of measured result. (Thus random errors can be evaluated through statistical analysis and can be reduced by averaging over a large number of observations).
5. They affect precision of results.
6. These errors are
produced by any one of a number of unpredictable and unknown
variations in the experiment.
Sources of Errors
(i) Caused by random
unpredictable fluctuations in experimental conditions like temperature,
moisture, vibration etc.
(ii) Limitations in
measurement process
(iii) Flexibility in setting
of apparatus
(iv) Carelessness of the observer
Minimization of Random errors
(i) Large number of replicate measurements i.e. repeating the observation a large number of times and taking the arithmetic mean of all the observations.
(ii)Better experiments (equipment, methodology, training analyst)
Examples of random errors
Answer Q1
Significant Figures Worksheet # 2
Q2. Find the number of significant figure in each of the following
measured values:
Significant Figures Worksheet # 3
Q3. Calculate the answers to the appropriate number of
significant figures:
(i) 23.7 x 3.8 (Answer; )
(ii) 45.76 x 0.25 (Answer; )
(iii) 81.04 x 0.010 (Answer; )
(iv) 6.47 x 64.5 (Answer; )
(v) 43.678 x 64.1 (Answer; )
(vi) 1.678 /0.42 (Answer; )
(vii) 28.367 /3.74 (Answer; )
(viii) 28.367 /3.74 (Answer; )
(ix) 4278/1.006 (Answer; )
Answers Q3
(i) 23.7 x 3.8 (Answer; 9.0 x 101)
(ii) 45.76 x 0.25 (Answer; 11)
(iii) 81.04 x 0.010 (Answer; 0.81)
(iv) 6.47 x 64.5 (Answer; 417)
(v) 43.678 x 64.1 (Answer; 2.80 x 103)
(vi) 1.678 /0.42 (Answer; 4.0)
(vii) 28.367 /3.74 (Answer; 7.58)
(viii) 28.367 /3.74 (Answer; 7.58)
(ix) 4278/1.006 (Answer; 4252)
Significant Figures Worksheet # 4
Q4. Round up the following up to three significant figures
(i) 34.216 g
(ii) 10.4107 m
(iii) 0.04597 mg
(iv) 2808 kg
(v) 0.0013979 L
(vi) 399.6879 kg
(vii) 989.8795 g
Answers Q4.
(i) 34.216 g (Answer; 34.2)
(ii) 10.4107 m (Answer; 10.4)
(iii) 0.04597 mg (Answer; 0.0460)
(iv) 2808 kg (Answer; 2810)
(v) 0.0013979 L (Answer; 0.00140 L)
(vi) 399.6879 kg (Answer; 4.00 x 102 kg)
(vii) 989.8795 g (Answer; 9.90 x 102 g)
Significant Figures Worksheet # 5
Q5. Round off each of the following correct up
to 3 significant figures:
(i) 56.4517 g
(ii) 8.20763 kg
(iii) 33.311 km
(iv) 50.099 cm
(v) 0.00124855 m
(vi) 498.876
(vii) 0.076489 mg
(viii) 258.7659 m
(ix) 2.8975
(x) 56789.75 kg
Answers Q5.
(i) 56.4517
g (Answer;56.5 g)
(ii) 8.20763 kg (Answer; 8.21
kg)
(iii) 33.311 km (Answer; 33.3
km)
(iv) 50.099 cm (Answer; 50.1
cm)
(v) 0.00124855 m (Answer; 0.00125 m)
(vi) 498.876 g (Answer; 499 g)
(vii) 0.076489 mg (Answer; 0.0765 mg)
(viii) 258.7659 m (Answer; 259 m)
(ix) 2.8975 km (Answer; 3.00 km)
(x) 56789.75 kg (Answer; 5.68 x 104 kg)
Significant Figures Worksheet # 6
Q6.Round the following to the specified degree of accuracy.
(i) 15.256 g correct to the three significant figures.(ii) 0.00838 mg correct to the two significant figures.
(iii) 0.004509 g correct to the one significant figures.
(iv) 29.404 mm correct to the four significant figures.
(v) 22.311 km correct to the four significant figures.
(vi) 3.0921 kg correct to the two significant figures.
(vii) 0.003519 mm correct to the one significant figures.
Answers Q6.
(i) 15.256 g correct to the three significant figures. (Answer;15.3 g)
(ii) 0.00838 mg correct to the two significant figures. (Answer;0.0084 mg)
(iii) 0.004509 g correct to the one significant figures. (Answer;0.005 g)
(iv) 29.404 mm correct to the four significant figures. (Answer;29.40)
(v) 22.311 km correct to the four significant figures. (Answer;22.31 km)
(vi)3.0921 kg correct to the two significant figures. (Answer;3.1 kg)
(vii) 0.003519 mm correct to the one significant figures.
(Answer;0.004 mm)
Significant Figures Worksheet # 7
Q7. Round the following to the specified degree of accuracy.
(i). 6.43 to 1 significant figure.(ii). 0.002515 to 1 significant figure.
(iii). 0.003663 to 1 significant figure
(iv). 49.806 to 2 significant figures
(v). 0.0072729 to 3 significant figures
(vi). 0.00733589 to 3 significant figures
(vii). 0.00533907 to 3 significant figures
(viii). 0.0002992979 to 1 significant figure
(ix). 12848.16 to 3 significant figures
(x). 0.026895889 to 2 significant figures
Answers Q7.
(i). 6.43 to 1 significant figure.
(ii). 0.002515 to 1 significant figure.
(iii). 0.003663 to 1 significant figure
(iv). 49.806 to 2 significant figures
(v). 0.0072729 to 3 significant figures
(vi). 0.00733589 to 3 significant figures
(vii). 0.00533907 to 3 significant figures
(viii). 0.0002992979 to 1 significant figure
(ix). 12848.16 to 3 significant figures
(x). 0.026895889 to 2 significant figures
Significant Figures Worksheet # 8
Q8. Round the following numbers
into four, three and two significant figures:
Answers Q8.
Significant Figures Worksheet # 9
Q9. Solve the following by applying rules of significant
figures:
Significant Figures Worksheet # 10
Q10. Calculate the answers to the appropriate number of
significant figures:
32.567 + 135.0 + 1.4567
(ii) 246.24 + 238.278 + 98.3 (iii) 658.0 + 23.5478 + 1345.29
Solution
Significant Figures Worksheet # 11
Q11.How
many significant figures should be present in the answer of the following
calculations?
scientific notation Worksheet # 12
Q12. Express the following in the scientific notation:
(i) 0.0048 (Answer; 4.8× 10–3)
(ii) 234,000 (Answer; 2.34 ×105)
(iii) 8008 (Answer; 8.008 ×103)
(iv) 500.0 (Answer; 5.000 × 102)
(v) 6.0012 (Answer; 6.0012 x 100)