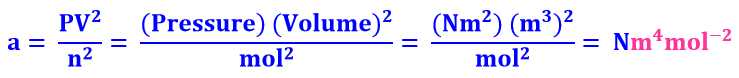Chemistry by Inam Jazbi: van Der Waal’s Equation

van Der Waal’s Equation

Definition

In order to modify the two conflicting postulates of the kinetic molecular theory regarding volumes and intermolecular attraction of gas molecules, a Dutch scientist Johannes Diderik (J. D.) van der Waal (1873) gave mathematical solution by the correction in molecular volume and intermolecular forces. This is known as van der Waal Equation.

It is the modification of the ideal gas law to take into account molecular size and molecular interaction forces.

The equation is considered as the updated version of the ideal gas equation that states that there are some point masses present in gases that undergo perfectly elastic collisions. However, the ideal gas law is incapable of explaining the behaviour of real gases. Due to this reason, the van der Waal’s equation was derived to define the physical state of a real gas.

Van der Waals introduced the size effect and the intermolecular attraction effect of the real gases. These two effects or factors in the Van der Waals equation are discussed under volume correction and pressure correction of the ideal gas equation and are arising because he considered the size and intermolecular attraction among the gas molecules.

The constants ‘a’ and ‘b’ have positive values and are characteristic of the individual gas. The van der Waals equation of state approaches the ideal gas law PV=nRT as the values of these constants approach zero. The constant ‘a’ provides a correction for the intermolecular forces. Constant ‘b’ is a correction for finite molecular size and its value is the volume of one mole of the atoms or molecules.

Kinetic theory of ideal gases assumes the gaseous particles as –

(i) Point masses without any volume,

(ii) Independent having no interactions (no forces of attraction or repulsion) and

(iii) Undergo perfectly elastic collisions.

In practice, van der Waals assumed that, gaseous particles –

(i) Are hard spheres.

(ii) Have definite volume and hence cannot be compressed beyond a limit.

(iii) Two particles at close range interact and have an exclusive spherical volume around them i.e. In case of real gases, both the forces of attraction as well as repulsion operate between gas molecules.

Note: If the gases obey the kinetic theory of gases, then they cannot be compressed since the attractions between the gas molecules is negligible.

Volume Correction in van der Waal’s Equation

Reason of Subtraction of Excluded Volume

real gas molecules are assumed to be a rigid hard sphere with definite volume. As the particles have a definite volume, the volume available for their movement is not the entire container volume but less. Therefore, the available volume for free movement of the gas molecules becomes less than the original molar volume or volume of the container (V_vessel). Volume in the ideal gas is hence an overestimation and has to be reduced for real gases.

Proof of Definite Volume of Gas Molecule

(When pressure is applied to a gas, the molecules come closer to each other. By continuous increase in pressure, a point is reached when molecules cannot further be compressed since repulsive forces are created. This indicates that gas molecules have definite volume. Although this is very small but not negligible).

Volume Correction by Subtracting Excluded Volume from Volume of vessel

The volume of a gas is the free space in the container in which molecules move about. Volume V of an ideal gas is the same as the volume of the container. The dot molecules of ideal gas have zero-volume and the entire space in the container is available for their movement.

The volume available for the gas molecules is less than the volume of the container, V.

Keeping in view the definite volume of gas molecules, van der Waal caluclated the actual volume (available volume) of a gas by subtracting excluded volume of ‘n’ moles of gas, ‘nb’ from the volume of the container (V_vessel). The volume of a real gas is, therefore, ideal volume minus the volume occupied by gas molecules.

Available volume = V = V_vessel – b (for 1 one molecule)

V = V_vessel – nb (for n mole )………………………… (i)

Where

V = free volume/actual volume (molar volume of ideal gas)

V_vessel= Volume of the vessel in which gas molecules are present

‘n’ = number of moles

‘b’ = volume correction factor/excluded volume/theoretical volume/Incompressible Volume of gas molecules per mole in highly compressed gaseous state. It is a constant and characteristic of gas, depends upon size of molecule.

The ideal gas equation can be written after correcting for this as:

P(V– nb ) = nRT

Excluded volume (‘b’) is not equal to actual volume of gas molecule. In fact, it is 4 times of actual volume of gas molecule.

‘b’ = 4V_molecule

Where, V_molecule is actual volume of one mole of a gas.

‘b’ = 4N_A x ⁴/₃ 𝜋r³

Where

N_A = Avogadro’s number

‘r’ = radius of molecule

For a given gas, the numerical vale of ‘a’ is greater than that of ‘b’.

Pressure correction in van der Waal’s Equation

The pressure of the gas is developed due to the wall collision of the gas molecules. We know that the intermolecular attraction comes into play when the molecules are brought close together by squeezing the gas. due to intermolecular attraction, the colliding molecules will experience an inward pull. Therefore, the pressures exerted by the molecules in real gases will be less than the ideal gases. The ideal gases have no intermolecular attraction. van der Waal also corrected the pressure produced by the molecules of the real gases. The higher the intermolecular attraction in the gas molecules greater is the magnitude of the pressure correction term. Therefore, the pressure correction term depends on the frequency of molecular collisions.

(Gaseous particles do interact. For inside particles, the interactions cancel each other. But, the particles on the surface and near the walls of the container do not have particles above the surface and on the walls. So, there will be net interactions or pulling of the bulk molecules towards the bulk that is away from the walls and surface. The molecules experiencing a net interaction away from the walls will hit the walls with less force and pressure. Hence, in real gases, the particles exhibit lower pressure than shown by ideal gases).

A molecule (A) in the interior of a gas is completely surrounded and attracted by the other gas molecules (B) on all sides. These attractive forces cancel out (The resultant attractive force on the molecule A due to all the surrounding B molecules is Zero). However, a molecule (A) about to strike the wall of the vessel is attracted by molecules on one side only, hence it experiences a net inward pull due to the attractive forces of B molecules. Therefore, it strikes the wall with reduced velocity.

The pressure of the real gas is less than the expected pressure due to attractions between the molecules. These attractions slow down the motion of gas molecules and result in:

i) reduction of frequency of collisions over the walls and

ii) reduction in the force with which the molecules strike the walls.

It means that pressure produced on the wall would be little bit lesser than pressure of an ideal gas molecule. Therefore, if observed pressure is simply indicated by P, ideal pressure P_i and less pressure P_L, then equation will be

P_{observed/real} or P = P_ideal – P_less(∴ P_ideal > P_real)

P = P_i – P_L

P_ideal = P_real + P_less

P_i = P + P_L ------------------------- (ii)

However, the reduction in pressure depends upon the number of particles (A and B) per unit volume i.e. is proportional to the square of molar concentration; n/V (one factor for reduction in frequency of collisions and the second factor for reduction in strength of their impulses on the walls).

[The average pressure exerted by the molecules decreased by P_L, which is proportional to the square of the density of gas molecules. Therefore, P_L a 1/V², since density a 1/V; ∴ P_L = a/V²]

P_L is pressure-correcting term for real gases, which is the pressure drop due to backward pull of striking molecules.

Where ‘a’ is a proportionality constant called van der Waals constant of attraction and is characteristic of a gas. Higher values of ‘a’ indicate greater attraction between gas molecules. The easily compressible gases like ammonia, HCl possess higher ‘a’ values. Greater the value of ‘a’ for a gas easier is the liquefaction.

Insert the value of P_L in equation (ii)

The corrected pressure and volume is now put in ideal gas equation to modify it, we get

This is van der Waal’s equation. Here ‘a’ and ‘b’ are van der Waal’s constants and contain positive values. The constants are the characteristic of the individual gas. When gas is ideal or that it behaves ideally then both the constant will be zero. Generally, ‘a’ constant help in the correction of the intermolecular forces while the ‘b’ constant helps in making adjustments for the volume occupied by the gas particles.

van der Waal’s Constant for some Common Real gases