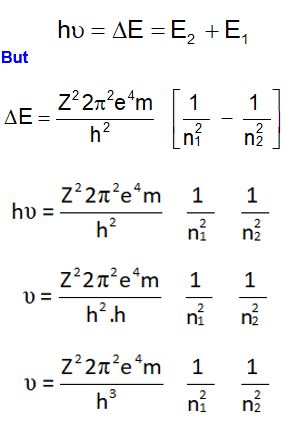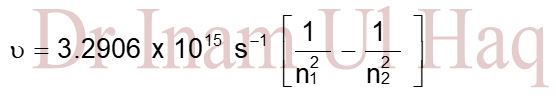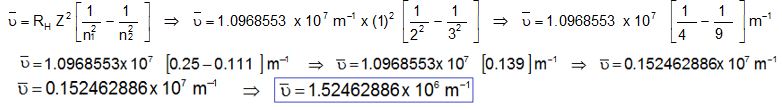Derivation of Radius of the nth Bohr’s Orbit for Hydrogen-Like Atoms (Single electron system)

Derivation of Radius of the n^th Bohr’s Orbit for Hydrogen-Like Atoms (Single electron system)   

Assumptions for Simple Atom

To derive an expression for radius, consider a hydrogen atom with atomic number equal to Z consisting of a single electron with charge –e and mass m revolving around the nucleus of charge +Ze (+e is charge of proton) with a tangential velocity v in an stationary orbit of radius r.

Electrostatic force of Attraction/Centripetal Force and Centrifugal force

Now the centrifugal and centripetal forces upon the revolving electron are given as:

Equating F_e and F_c

At uniform circular equilibrium motion, these two opposite forces must be equal to each other i.e.

 

Determination of v² of electron by using Bohr’s Postulate

According to Bohr’s postulate, angular momentum of electron revolving around the nucleus is an integral multiple of h/2p.

Calculation of Radius (r)

Substituting the value v² from equation (ii) in equation (i)

 

Calculation of n^th Bohr’s orbit (r_n)

The above equation shows that radius of orbit is directly proportional to the square of the principal quantum numbers (r α n² i.e. 1, 2, 3, ……..) and inversely proportional to atomic number. As the value of n increases, the radius of the orbit will increase.

 

 

Derivation of Energy of the n^th Bohr’s Orbit

Basic of Derivation

The total energy of an electron revolving in any orbit around the nucleus is given by,

Calculation of K.E

The K.E. of electron with mass m revolving around the nucleus with velocity v is given by the following expression;

Now the centrifugal and centripetal forces upon the revolving electron are given as:

 

Now the centrifugal and centripetal forces upon the revolving electron are given as:

At uniform circular equilibrium motion, these two opposite forces must be equal to each other i.e.

Calculation of P.E Using Definition of Work

Calculation of Total Energy

As we know that

Put the value of “r” from equation (iii) to equation (ii)

E is always negative. Negative sign shows that the electron is bound to the atom and energy must be spent in order to remove it from the orbit.

All energy states are bound states as the negative sign indicates. When n = 1; this corresponds to electron at the closest possible distance from the nucleus and at its lowest energy and is called ground state energy. All energy states with value of n higher than 1 are termed as excited states. When n = α then E = 0; which means that the system is unbound and the electron is free. It should be noted that the energy is increasing as the n (orbits) increasing; however the difference of energy between two orbits is decreasing.

 

Conclusion

If total energy = - x

Then

KE = + x

PE = - 2x

 

  

Expression for ∆E of Electronic Transition between Orbits

Calculation of ∆E

To calculate the energy emitted by atom in the form of radiation

when an electron jumps from a higher energy state n₁; let us make

use of the postulate of Bohr’s model; according to which:

 

Expression for Frequency of Electronic Transition between Orbits

To calculate the frequency of emitted radiations (or photons there in); let us make use of the Bohr’s postulate; according to which:

Expression for Wave Number and Wave Length of Radiation

This is the expression to calculate wave number and wavelength of radiation emitted during electronic transitions (i.e. when electron drop from higher energy state to lower energy state).

 

 

Q1. Calculate the wave number and wavelength of Balmer series of hydrogen spectrum in which electron jumps from orbit 3 to orbit 2.

Solution

Calculation of Wave Number

Here;

R_H = 1.0968553 x 10⁷ m^-1

n₁ = 2

n₂ = 3

Z  = 1

Calculation of Wave Length 

Q2. What is the wavelength and wave number of radiation that is emitted when a hydrogen atom undergoes a transition from orbit 3 to orbit 1.

Solution

Calculation of Wave Number 

R_H = 1.0968553 x 10⁷ m^-1

n₁ = 1

n₂ = 3

Q3.Calculate the ratio of radius of second and third orbit of hydrogen atom. (Bohr’s radius =  0.529ºA)

Solution 

Q4. If the radius of first Bohr orbit is ‘x’ then calculate the radius of the third orbit of hydrogen.

Solution 

Q1.Calculate the energy of the electron in theground state and first excited state of the hydrogen atom

Solution

Part (A)

Z for H = 1

n for ground state = 1